Your questions
In “Elastic Chains” chapter, going from eqn. (69) to eqn. (70)
- $\langle\rho_q \rho_{-q}\rangle$ has form
$$ \exp(i\Delta q a[j-k])\, \left|j-k\right|^{-2\pi\ell_\text{osc}^2/a^2} $$
- This leads to the conclusion $$ \bra{0} \rho_q \rho_{-q} \ket{0} \sim \left(\Delta q\right)^{-1+2\pi\ell_\text{osc}^2/a^2}. $$
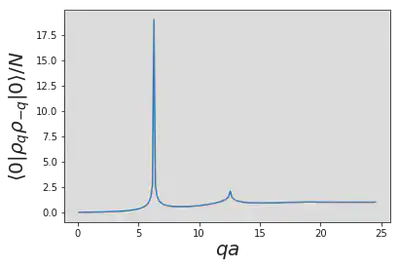
What we are supposed to conclude about the Bragg peaks?
Converting between second quantization and many-body wavefunction pictures
Could we go through a couple of examples of this (e.g. single particle density matrix, correlation functions)?
$$ \psi(\br)\longleftrightarrow \adop(\psi)\ket{\text{VAC}}. $$
$$ \Psi^{\text{S}}(\br_1,\ldots,\br_N) \longleftrightarrow \adop(\psi_1)\cdots \adop(\psi_N)\ket{\text{VAC}}. $$
$$ \Psi^{\text{S}}(\br_1,\ldots,\br_N) = \frac{1}{\sqrt{N!}}\sum_P\psi_1(\mathbf{r}_{P_1})\psi_{2}(\mathbf{r}_{P_2})\cdots\psi_{N}(\mathbf{r}_{P_N}) $$
If $\ket{\Psi}$ has wavefunction $\Psi(x_1,\ldots, x_N)$, then $\pop(X)\ket{\Psi}$ has $N-1$ particle wavefunction
$$ \sqrt{N}\Psi(X,x_1,\ldots, x_{N-1}) $$
Proof for product state:
$$ \begin{align*} &\Psi(X)\adop(\psi_1)\cdots \adop(\psi_N)\ket{\text{VAC}}\\ &= \sum_{n=1}^N\psi_n(X)\overbrace{\adop(\psi_1)\cdots \adop(\psi_N)}^{n \text{ missing}}\ket{\text{VAC}}\\ &\longleftrightarrow \frac{1}{\sqrt{(N-1)!}}\sum_{n=1}^N\sum_{P\in S_{N-1}}\psi_n(X)\overbrace{\psi_{P_1}(x_1)\psi_{P_2}(x_2)\cdots\psi_{P_N}(x_{N-1})}^{\psi_n \text{ missing}}\\ &= \frac{\sqrt{N}}{\sqrt{N!}}\sum_{P\in S_{N}}\psi_{P_1}(x_1)\psi_{P_2}(x_2)\cdots\psi_{P_N}(x_N),\text{ with } x_N=X\\ &=\sqrt{N}\Psi^{\text{S}}(x_1,\ldots,x_{N-1}, X) \end{align*} $$
Example 1: density matrix
Apply to single particle density matrix
$$ g(\br,\br’) \equiv N \int d\br_{2}\cdots d\br_{N},\Psi^{*}(\br,\br_{2},\ldots,\br_{N})\Psi(\br’,\br_{2},\ldots,\br_{N}) $$
This can be written in terms of our field operators as
$$ g(\br,\br’)= \braket{\Psi|\pdop(\br)\pop(\br’)|\Psi} $$
Example 2: correlation functions
$$ \rho_2(x_1,x_2) = N(N-1) \int dx_3\ldots dx_N ,\left|\Psi(x_1,x_2,\ldots,x_N)\right|^2 $$
$$ \rho_2(x,y) =\braket{\Psi|\pdop(x)\pdop(y)\pop(y)\pop(x)|\Psi} $$
Equation (27) in “B is for Bunching”
Show that the density matrix
$$ \rho=\int_0^{2\pi}\frac{d\theta}{2\pi}\ket{\bar N_L,\bar N_R}_\theta\bra{\bar N_R,\bar N_L}_\theta $$
coincides with that of a mixture of Fock states with binomial distribution of atoms into states $\varphi_{L}$, $\varphi_{r}$
$$ \ket{N_L,N_R}\equiv\frac{1}{\sqrt{N_L! N_R!}}\left(\adop_L\right)^{N_L}\left(\adop_R\right)^{N_R}\ket{\text{VAC}}. $$
Review derivation of the Bogliubov Hamiltonian
Three steps
Split Hamiltonian according to number of occurrences of $\adop_0$, $\aop_0$
Do some bookkeeping
Replace $\adop_0$, $\aop_0$ with $\sqrt{N}$
Split Hamiltonian
$$ H =\sum_\bk \epsilon(\bk)\adop_\bk\aop_\bk + \overbrace{\frac{U_0}{2V}\sum_{\bk_1+\bk_2=\bk_3+\bk_4} \adop_{\bk_1}\adop_{\bk_2}\aop_{\bk_3}\aop_{\bk_4}}^{\equiv H_\text{int}} $$
$$ \begin{align*} H_\text{int} = &\frac{U_0}{2V}\adop_0\adop_0\aop_0\aop_0 \\ &+\frac{U_0}{2V}\sum_{\bk\neq0}\left[\adop_{\bk}\adop_{-\bk}\aop_{0}\aop_{0} + \adop_{0}\adop_{0}\aop_{\bk}\aop_{-\bk}+4\adop_\bk\adop_0\aop_0\aop_\bk\right]\\ &+\frac{U_0}{V}\sum_{\substack{\bk_1=\bk_2+\bk_3\\ \bk_{1,2,3}\neq 0}}\left[\adop_{\bk_3}\adop_{\bk_2}\aop_{\bk_1}\aop_0 +\adop_0\adop_{\bk_1}\aop_{\bk_2}\aop_{\bk_3}\right]\\ &+\frac{U_0}{2V}\sum_{\substack{\bk_1+\bk_2=\bk_3+\bk_4\\ \bk_{1,2,3,4}\neq 0}} \adop_{\bk_1}\adop_{\bk_2}\aop_{\bk_3}\aop_{\bk_4}. \end{align*} $$
Bookkeeping
$$ \adop_0\adop_0\aop_0\aop_0 = N(N-1) - 2N'N_0+O(N_0^0 ). $$
$$ \begin{align*} H_\text{pair} = &N\epsilon(0)+\frac{U_0}{2V}N(N-1) \nonumber\\ &+\sum_{\bk\neq 0}\left(\left[\epsilon(\bk)-\epsilon(0)\right]\adop_\bk\aop_\bk\right.\\ &\left.+\frac{U_0}{2V}\left[\adop_{\bk}\adop_{-\bk}\aop_{0}\aop_{0} + \adop_{0}\adop_{0}\aop_{\bk}\aop_{-\bk}+2\adop_\bk\adop_0\aop_0\aop_\bk\right]\right) \end{align*} $$
Replace $\adop_0$, $\aop_0$ with $\sqrt{N}$
Recall Schwinger bosons (PS1)
$$ \begin{align*} S^x &= \frac{1}{2}\left(\adop\bop+\bdop\aop\right)\nonumber\\ S^y &= \frac{i}{2}\left(-\adop\bop+\bdop\aop\right)\nonumber\\ S^z &= \frac{1}{2}\left(\adop\aop-\bdop\bop\right) \end{align*} $$
can be used to derive
$$ \begin{align*} s^+ &=\sqrt{2s}\sqrt{1-\frac{\adop\aop}{2s}}\aop \\ s^- &= \sqrt{2s}\adop\sqrt{1-\frac{\adop\aop}{2s}} \\ s^z &= \left(s - \adop \aop\right). \end{align*} $$
What is a quasiparticle?
Why does the excited state have two contributions?
“Dressed” nature of quasiparticles.