The Elastic Chain
Simple model of quantum solid
Quantum fluctuations change character of crystalline order
The career of a young theoretical physicist consists of treating the harmonic oscillator in ever-increasing levels of abstraction.
$$ \nonumber \newcommand{\br}{\mathbf{r}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bq}{\mathbf{q}} \newcommand{\bv}{\mathbf{v}} \newcommand{\pop}{\psi^{\vphantom{\dagger}}} \newcommand{\pdop}{\psi^\dagger} \newcommand{\Pop}{\Psi^{\vphantom{\dagger}}} \newcommand{\Pdop}{\Psi^\dagger} \newcommand{\Phop}{\Phi^{\vphantom{\dagger}}} \newcommand{\Phdop}{\Phi^\dagger} \newcommand{\phop}{\phi^{\vphantom{\dagger}}} \newcommand{\phdop}{\phi^\dagger} \newcommand{\aop}{a^{\vphantom{\dagger}}} \newcommand{\adop}{a^\dagger} \newcommand{\bop}{b^{\vphantom{\dagger}}} \newcommand{\bdop}{b^\dagger} \newcommand{\cop}{c^{\vphantom{\dagger}}} \newcommand{\cdop}{c^\dagger} \newcommand{\bra}[1]{\langle{#1}\rvert} \newcommand{\ket}[1]{\lvert{#1}\rangle} \newcommand{\inner}[2]{\langle{#1}\rvert #2 \rangle} \newcommand{\braket}[3]{\langle{#1}\rvert #2 \lvert #3 \rangle} \newcommand{\sgn}{\mathrm{sgn}} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\E}{\mathbb{E}} \newcommand{\brN}{\br_1, \ldots, \br_N} $$
Hamiltonian
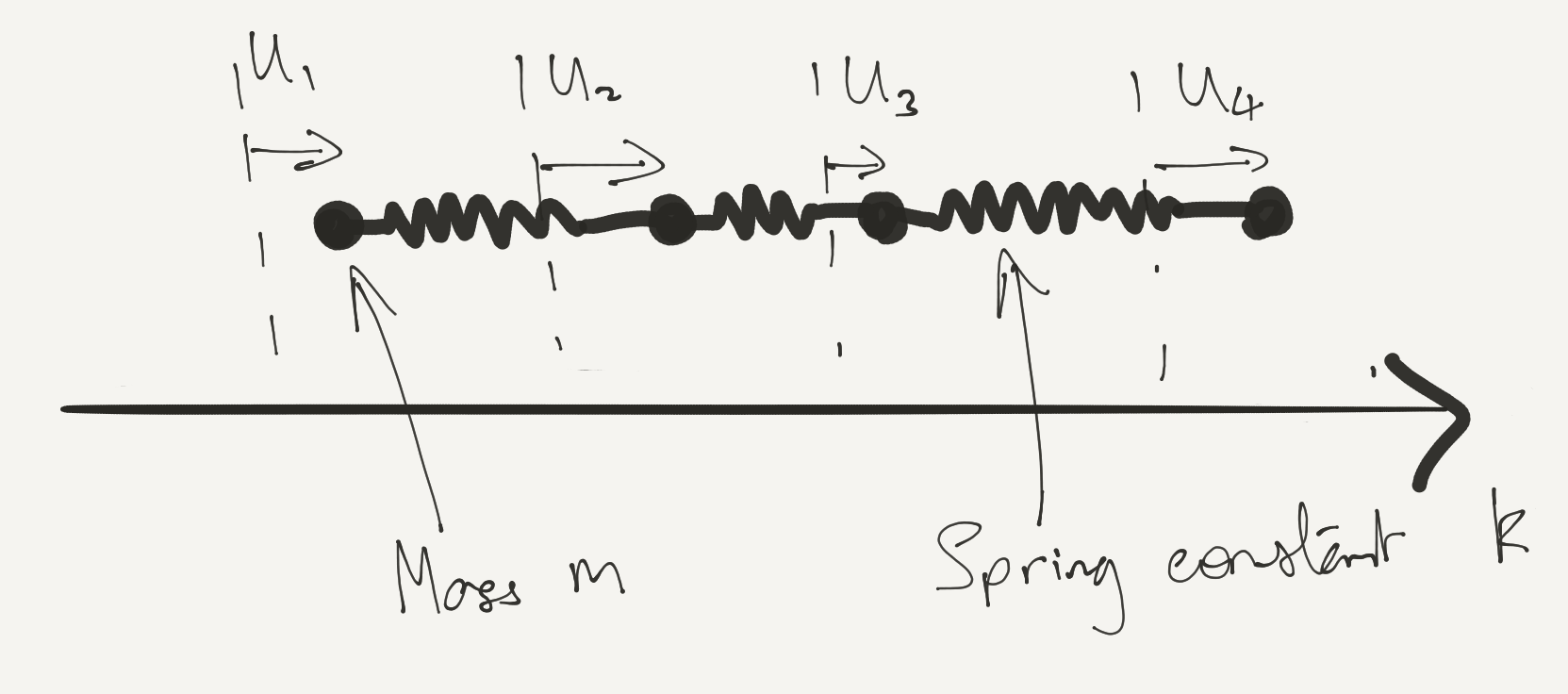
$$ \label{coll_Hchain} H = \sum_{j=1}^N \left[\frac{p_j^2}{2m} + \frac{k}{2} (u_j-u_{j+1})^2 \right]. $$
Identify $u_j=u_{N+j}$
Let’s look at the classical system first
Equations of Motion
$$ m \ddot u_j = k(u_{j-1} + u_{j+1} - 2u_j). $$
- Look for oscillatory solutions $u_j(t) = u_j e^{-i\omega t}$
$$ -\omega^2 \begin{pmatrix} u_1 \\ u_2 \\ \cdots \\ u_{N-1}\\ u_N \end{pmatrix} = \frac{k}{m} \begin{pmatrix} -2 & 1 & 0 & \cdots & 1 \\ 1 & -2 & 1 & \cdots & 0\\ \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & \cdot & 1 & -2 & 1\\ 1 & 0 & \cdots & 1 & -2 \end{pmatrix} \begin{pmatrix} u_1 \\ u_2 \\ \cdots \\ u_{N-1}\\ u_N \end{pmatrix} $$ - Eigenvectors given by plane waves $u_j = (z_n)^j$, where $z_n$ $$ z_n = \exp\left(\frac{2\pi i n}{N}\right),\qquad n = 0,\ldots, N-1. $$
- Let’s take $N$ odd and index $z_n$ using positive and negative
$$ z_n = \exp\left(\frac{2\pi i n}{N}\right),\qquad n = -(N-1)/2,\ldots, (N-1)/2. $$
- Write $\eta_n\equiv \frac{2\pi n}{N}$, so that eigenstates are $u_j=\exp(i\eta_n j)$
By substituting into the equation of motion show that the dispersion relation is $$ \omega(\eta) = \sqrt{\frac{4k}{m}}\left|\sin\eta/2\right|. \label{coll_Dispersion} $$
Dispersion
$$ \omega(\eta) = \sqrt{\frac{4k}{m}}\left|\sin\eta/2\right|. $$
- $\omega(\eta)\to 0$ as $\eta\to 0$. $\eta=0$ mode corresponds to translation
- At small $\eta$ dispersion is linear, as we expect for sound waves.
General solution
Expressed as superposition of normal modes $$ u_j(t) = \frac{1}{\sqrt{N}}\sum_{|n| \leq (N-1)/2} q_n(t) e^{i\eta_n j} \label{coll_modes} $$
Important $q_{-n}=q^*_n$ ensures that $u_j$ is real
Time dependence $$ q_n(t) = \alpha_n e^{-i\omega(\eta_n) t} + \beta_n e^{i\omega(\eta_n) t} $$
$q_0(t) = \sqrt{N}(X+Vt)$ describes the motion of the centre of mass.
Hamiltonian formulation
Write momenta in terms of Fourier modes $$ p_j(t) = \frac{1}{\sqrt{N}}\sum_{|n| \leq (N-1)/2} \pi_n(t) e^{-i\eta_n j}, \label{coll_Pexp} $$
Note change of sign in exponent! If $u_j$, $p_j$ are canonical variables $\{u_j, p_k\}=\delta_{jk}$, then $\{q_m,\pi_n\}=\delta_{mn}$.
Show that in terms of the Fourier modes $$ H = \sum_{|n| \leq (N-1)/2} \left[\frac{1}{2m}\pi_n \pi_{-n} + k (1-\cos \eta_n) q_n q_{-n}\right]. \label{coll_HDiag} $$
$$ \begin{align} T = \sum_{j=1}^N \frac{p_j^2}{2m} = \frac{1}{2mN}\sum_{j=1}^N\left(\sum_{|n| \leq (N-1)/2} \sum_{|m| \leq (N-1)/2}\pi_n e^{-i\eta_n j} \pi_m e^{-i\eta_m j}\right) \end{align} $$
- Key idea
$$ \sum_{j=1}^N e^{-i(\eta_n+\eta_m) j}= N\delta_{n,-m} $$
$$ T = \frac{1}{2m}\sum_{|n| \leq (N-1)/2} \pi_n \pi_{-n} $$
System of oscillators
- Could split amplitudes into real and imaginary parts
$$ \begin{align} q_n &= \frac{1}{\sqrt{2}}\left(q_n' + i q_n''\right),\quad q_{-n} = \frac{1}{\sqrt{2}}\left(q_n' - i q_n''\right)\\ \pi_n &= \frac{1}{\sqrt{2}}\left(\pi_n' + i \pi_n''\right),\quad \pi_{-n} = \frac{1}{\sqrt{2}}\left(\pi_n' - i \pi_n''\right),\quad n\geq 0. \label{coll_RandI} \end{align} $$The Hamiltonian is then$H=H' + H''$with $$ H’ = \sum_{0 < n \leq (N-1)/2} \left[\frac{1}{2m}\pi’n \pi’{n} + k (1-\cos \eta_n) q’n q’{n}\right]. $$ - Compare with usual SHO: read off dispersion relation
Complex Coordinates
$$ \begin{equation} a = \sqrt{\frac{m\omega}{2}}\left(x + \frac{i}{m\omega} p \right) \label{a_def} \end{equation} $$ $$ H = \omega \left|a\right|^2 $$
- Hamilton’s equations are
$$ \begin{align} \dot a &= -i \frac{\partial H}{\partial a^*}= -i\omega a\\ \dot a^* &= i \frac{\partial H}{\partial a} = i\omega a^* \end{align} $$
- Solution $a(t) = e^{-i\omega t} a(0)$
Complex coordinates: normal modes
$$ \begin{align} a_n &= \sqrt{\frac{m\omega(\eta_n)}{2}}\left(q_n + \frac{i}{m\omega(\eta_n)}\pi_{-n}\right)\nonumber\\ a^*_n &= \sqrt{\frac{m\omega(\eta_n)}{2}}\left(q_{-n} - \frac{i}{m\omega(\eta_n)}\pi_{n}\right),\qquad n\neq 0 \label{coll_adef} \end{align} $$
$$ \begin{align} q_n &= \sqrt{\frac{1}{2m\omega(\eta_n)}}\left(a_n + a_{-n}^*\right)\nonumber\\ \pi_n &= -i\sqrt{\frac{m\omega(\eta_n)}{2}}\left(a_{-n} - a_{n}^*\right) \end{align} $$
$$ \begin{align} q_n &= \sqrt{\frac{1}{2m\omega(\eta_n)}}\left(a_n + a_{-n}^*\right)\nonumber\\ \pi_n &= -i\sqrt{\frac{m\omega(\eta_n)}{2}}\left(a_{-n} - a_{n}^*\right),\\ H &= \sum_{|n| \leq (N-1)/2} \left[\frac{1}{2m}\pi_n \pi_{-n} + k (1-\cos \eta_n) q_n q_{-n}\right] \end{align} $$
- $H$ in terms of $a_n$, $a_n^*$ $$ H = \frac{\pi_0^2}{2m}+\sum_{\substack{n\neq 0 \ |n| \leq (N-1)/2}} \omega(\eta_n) \left|a_n\right|^2, $$
- First term is (free) centre of mass.
Quantum Oscillators
$a$, $a^*\longrightarrow\aop$, $\adop$ satisfying $[\aop,\adop]=1$ $$ H = \frac{\omega}{2}\left(\adop\aop+\aop\adop\right). $$
- Key property is $$ \begin{align} \left[\aop, H\right] &= \omega\aop,\\ \left[\adop, H\right] &= -\omega \adop. \end{align} $$
- If $\ket{\psi}$ is an eigenstate of the Hamiltonian $H \ket{\psi} = E \ket{\psi}$ then $\adop\ket{\psi}$ is an eigenstate with energy $E+\omega$ $$ H \adop \ket{\psi} = \adop H \ket{\psi} + [H, \adop] \ket{\psi} = \left(E+\omega\right)\adop\ket{\psi}. $$
Similarly $a\ket{\psi}$ is an eigenstate with energy $E-\omega$
Unless $\aop\ket{\psi}=0$, in which case $\ket{\psi}=\ket{0}$, the ground state
As a result $$ \ket{n} = \frac{1}{\sqrt{n!}}\left(\adop\right)^n\ket{0}. $$ The factor of $\frac{1}{\sqrt{n!}}$ normalizes the state
The ground state has energy $E_0=\omega/2$.
The Quantum Chain
- We have operators $[\aop_m,\adop_n]=\delta_{mn}$, and Hamiltonian $$ H = \frac{\pi_0^2}{2m}+\sum_{\substack{n\neq 0 \ |n| \leq (N-1)/2}} \frac{\omega(\eta_n)}{2}\left(\adop_n\aop_n+\aop_n\adop_n\right). $$
- General energy eigenstate may be written
$$ \begin{align} \ket{\mathbf{N}} &= \prod_{\substack{n\neq 0 \\ |n| \leq (N-1)/2}} \frac{\left(\adop_n\right)^{N_n}}{\sqrt{N_n!}} \ket{0}\\ E(\mathbf{N}) &= \overbrace{\frac{1}{2}\sum_{|n| \leq (N-1)/2} \omega(\eta_n)}^{\equiv E_0} + \sum_{\substack{n\neq 0 \\ |n| \leq (N-1)/2}} \omega(\eta_n) N_n \end{align} $$
Oscillator Quanta are Bosons!
Eigenstates labelled by occupation numbers
Energy is additive $$ E(\mathbf{N}) = E_0 + \sum_{\substack{n\neq 0 \ |n| \leq (N-1)/2}} \omega(\eta_n) N_n $$
These are not the particles making up the chain!
Thermodynamic ($N\to \infty$) limit
- Expect to find extensive energy, proportional to system size $$ e_0 = \lim_{N\to \infty} \frac{E_0}{N} $$
- Separation of $\eta_n$ values is $2\pi/N$, so $$ \sum_{|n| \leq (N-1)/2} \left(\cdots\right) \xrightarrow{N\to\infty} N \int_{-\pi}^\pi \frac{d\eta}{2\pi}\left(\cdots\right). $$ so $$ e_0 = \int_{-\pi}^\pi\frac{d\eta}{2\pi} \frac{\omega(\eta)}{2} = \sqrt{\frac{k}{2m}}\int_{-\pi}^\pi\frac{d\eta}{2\pi} \sqrt{1-\cos \eta}=\frac{2}{\pi}\sqrt{\frac{k}{m}}. $$
Continuum ($a \to 0$) limit
- 1D elastic modulus is $$ \kappa \equiv \frac{\text{tension}}{\text{strain}}=\frac{k\Delta x}{\Delta x/a} = ka $$
- $k/m =k/(\rho a)= \kappa/(\rho a^2)$, where $\rho$ is mass / length $$ \frac{E_0}{L} =\frac{2}{\pi}\sqrt{\frac{k}{m}}\frac{N}{L} = \frac{2}{\pi}\sqrt{\frac{\kappa}{\rho}}\left(\frac{N}{L}\right)^2 $$
- Energy per unit length diverges as $N\to\infty$
Potential energy can be written $$ V = \frac{k}{2} \sum_j^N (u_j-u_{j+1})^2 \xrightarrow{N\to\infty} \frac{\kappa}{2} \int_0^L dx \left[u’(x)\right]^2. $$
Define the Fourier modes slightly differently $$ u(x) = \sum_{n=-\infty}^\infty u_n e^{ik_n x}, $$ where $k_n =2\pi n/L$. Note that $k_n x = \eta_n j$. $$ V=\frac{\kappa L}{2}\sum_n k_n^2 u_nu_{-n} $$
Defining the momentum density $\pi(x=ja) = p_j N/L$, then $$ \left[u(x),\pi(x’)\right]=i\delta(x-x’), $$ $$ T = \sum_{j=1}^N \frac{p_j^2}{2m} = \frac{1}{2\rho}\int_0^L dx\left[\pi(x)\right]^2. $$
Use mode expansion
$$ \pi(x) = \lim_{N\to\infty} \frac{p_{j=xN/L}N}{L} =\frac{1}{L}\sum_{n=-\infty}^\infty \pi_n e^{-2\pi i nx /L}, $$
$$ T= \frac{1}{L}\sum_{n=-\infty}^\infty \frac{1}{2\rho} \pi_n\pi_{-n} $$
Continuum Hamiltonian $H= T+V$ $$ H = \sum_{n=-\infty}^\infty \left[\frac{1}{2\rho L} \pi_n\pi_{-n} + \frac{\kappa L k_n^2}{2} u_nu_{-n} \right]. $$
We can now read off the dispersion relation $$ \omega(k) = c|k|, $$ where $c=\sqrt{\frac{\kappa}{\rho}}$ is the speed of sound
Lattice was origin of periodic dispersion. Now it has gone
- Transcribing the definition of the oscillator variables
$$ \begin{align} a_n &= \frac{1}{\sqrt{2}}\left[\sqrt{ZkL} u_n + \frac{i}{\sqrt{ZkL}}\pi_{-n}\right]\nonumber\\ a^*_n &= \frac{1}{\sqrt{2}}\left[\sqrt{ZkL} u_{-n} - \frac{i}{\sqrt{ZkL}}\pi_{n}\right]. \end{align} $$$Z\equiv\sqrt{\kappa\rho}$ is impedance $$ H - E_0 = \sum_{n=-\infty}^\infty c\left|k_n\right|\adop_n\aop_n. \label{coll_excess} $$
Finite Temperature
Occupancies thermal averages given by Bose function ($\beta=\frac{1}{k_\text{B}T}$) $$ \langle N_n \rangle = n_\text{B}(\omega(\eta_n))\equiv \frac{1}{\exp\left(\beta\omega(\eta_n)\right)-1}, \label{coll_Bose} $$
Average energy is finite due to exponential tail of $n_\text{B}(\omega)$ $$ \langle H - E_0 \rangle =\sum_{|n|\leq (N-1)/2} \omega(\eta_n)n_\text{B}(\omega(\eta_n)). $$
At low energies $n_{\text{B}}(\omega) \sim \frac{1}{\beta\omega}$ and contribution of each mode is $$ \omega n_\text{B}(\omega) \xrightarrow{\omega\to 0} k_\text{B}T, $$
Position Fluctuations
Classical: regular arrangement of masses (+ thermal fluctuations)
Quantum: $u_j-u_k$ fluctuates, even in ground state
$$ \bra{0}\left(u_j-u_k\right)^2\ket{0}\neq 0. \label{coll_gsfluct} $$
- Write displacements in $\aop_n$, $\adop_{n}$, then evaluate expectation
$$ \begin{align} u_j &= \frac{1}{\sqrt{N}}\sum_{|n| \leq (N-1)/2} q_n e^{i\eta_n j}\\ q_n &= \sqrt{\frac{1}{2m\omega(\eta_n)}}\left(a_n + a_{-n}^\dagger\right) \end{align} $$
- Result:
$$ \begin{multline} \bra{0}\left(u_j-u_k\right)^2\ket{0} \\ = \frac{1}{2mN} \sum_{|n| \leq (N-1)/2} \frac{1}{\omega(\eta_n)} \left[e^{i\eta_n j}- e^{i\eta_n k}\right]\left[e^{-i\eta_n j}- e^{-i\eta_n k}\right] \end{multline} $$ $N\to\infty$ limit
$$ \begin{align} \bra{0}\left(u_j-u_k\right)^2\ket{0} &= \frac{1}{mN}\sum_{|n| \leq (N-1)/2} \frac{1-\cos\left(\eta_n[j-k]\right)}{\omega(\eta_n)}\\ &= \frac{1}{m}\int_{-\pi}^\pi \frac{d\eta}{2\pi} \frac{1-\cos\left(\eta[j-k]\right)}{\omega(\eta)}. \label{coll_uvar} \end{align} $$
$$ \bra{0}\left(u_j-u_k\right)^2\ket{0} = \frac{1}{m}\int_{-\pi}^\pi \frac{d\eta}{2\pi} \frac{1-\cos\left(\eta[j-k]\right)}{\omega(\eta)} $$
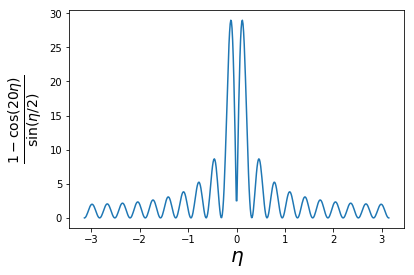
Show that as $\left|i-j\right|\to\infty$
$$ \bra{0}\left(u_i-u_j\right)^2\ket{0} \sim \frac{\ell_\text{osc}^2}{\pi} \log \left|i-j\right| \label{coll_LogFluct} $$
where
$\ell_\text{osc}\equiv\left(km\right)^{-1/4}$is the oscillator length
Uncertainty in the separation of two masses increases with separation.
Ground state of chain not a crystal; more closely resembles fluid
Conclusion depends on dimension (crytals do exist in 3D!)
Density Fluctuations
Alternatively, consider fluctuations of density $$ \rho(x) = \sum_{j=1}^N \delta_L(x-x_j), $$ $x_j = ja + u_j$, and $\delta_L(x)$ is $L$-periodic version of $\delta$-function
Fourier components $$ \rho_k = \sum_{j=1}^N\exp(-i k x_j) $$
$$ \rho_k = \sum_{j=1}^N\exp(-i k x_j). $$
In ordered configuration $x_j = ja$, we have
$$ \rho_{k_n=2\pi n/L} = \begin{cases} N & n = 0 \mod N \\ 0 & \text{ otherwise.} \end{cases} $$Bragg peaks at multiples of $\frac{2\pi}{a}$ observed in diffraction experiments
Translation of lattice changes phase of $\rho_k$, so $|\rho_k|^2$ unchanged
- What about quantum ground state? We should evaluate $$ \bra{0} \rho_q \rho_{-q} \ket{0} = \sum_{j,k=1}^N \bra{0} \exp(iq[x_j-x_k])\ket{0}. \label{coll_Struct} $$ Upon substituting the mode expansion we get expressions of form $$ \bra{0} \exp(\lambda \aop + \mu \adop)\ket{0}. $$
Prove the Hadamard Lemma
$$ \begin{align} e^{A}B e^{-A} &= B + \left[A,B\right] + \frac{1}{2!}\left[A,\left[A,B\right]\right]+\frac{1}{3!}\left[A,\left[A,\left[A,B\right]\right]\right]+\ldots \\ &\equiv e^{\left[A,\cdot\right]}B, \end{align} $$[Hint: Consider the differential equation in $x$ obeyed by $e^{xA}B e^{-xA}$]
Show that the exponent can be written in a form with all occurrences of $\adop$ to the left of all $\aop$ (this operation is called normal ordering; we will meet it again).
$$ \exp(\lambda \aop + \mu \adop) = \exp(\lambda \mu /2) \exp(\mu\adop)\exp(\lambda\aop). $$ [Hint: Consider the differential equations obeyed by $F_1(s)=e^{s(A+B)}$ and $F_2(s)=e^{sA}e^{sB}$]
- Using $\bra{0} \exp(\lambda \aop + \mu \adop)\ket{0} = \exp(\lambda \mu /2)$ we get
$$ \begin{equation} \begin{split} \bra{0} \rho_q \rho_{-q} \ket{0} = \sum_{j,k=1}^N &\exp(iqa[j-k])\\ &\times\exp\left(-\frac{q^2}{2mN}\sum_{|n| \leq (N-1)/2} \frac{1-\cos\left(\eta_n[j-k]\right)}{\omega(\eta_n)}\right). \end{split} \end{equation} $$
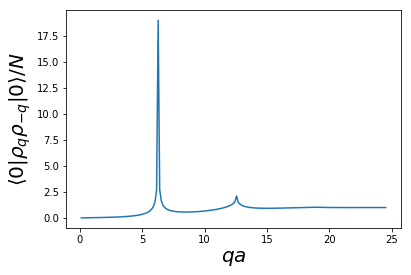
- Have seen expression in exponent before!
$$ -\frac{q^2}{2mN}\sum_{|n| \leq (N-1)/2} \frac{1-\cos\left(\eta_n[j-k]\right)}{\omega(\eta_n)}\sim - \frac{2\pi\ell_\text{osc}^2}{a^2}\log|j-k| $$
- Near first Bragg peak at $q=2\pi/a$ $$ \exp(i\Delta q a[j-k])\left|j-k\right|^{-2\pi\ell_\text{osc}^2/a^2}, $$ where $\Delta q$ is deviation from $2\pi/a$. This implies $$ \bra{0} \rho_q \rho_{-q} \ket{0} \sim \left(\Delta q\right)^{-1+2\pi\ell_\text{osc}^2/a^2}. $$