Superconductivity

• Bardeen, Cooper and Schrieffer’s (BCS) theory of superconductivity

• Idea: electrons in a superconductor bind to form Cooper pairs that behave like bosons

• The phenomena of superconductivity and superfluidity are closely linked: superconductor is ’like’ BEC of Cooper pairs

• Same Hamiltonian as before

$$ H = \int d\br\left[ \sum_{s=\uparrow,\downarrow}\frac{1}{2m}\nabla\pdop_s\cdot\nabla\pop_s + U_0 \pdop_\uparrow\pdop_\downarrow\pop_\downarrow\pop_\uparrow\right] $$

• For a pair of particles of opposite spin, this is equivalent to

$$ H = -\frac{1}{2m}\left[\nabla_1^2+\nabla_2^2\right] + U_0\delta(\br_1-\br_2) $$

• For $U_0<0$ and sufficiently large, expect a bound state to form with a symmetric spatial wavefunction and a spin singlet

Discussion: Cooper’s problem

The BCS Wavefunction

In momentum space our Hamiltonian is

$$ H =\sum_{\bk,s} \epsilon(\bk)\adop_{\bk,s}\aop_{\bk,s} + \overbrace{\frac{U_0}{V}\sum_{\bk_1+\bk_2=\bk_3+\bk_4} \adop_{\bk_1,\uparrow}\adop_{\bk_2,\downarrow}\aop_{\bk_3,\downarrow}\aop_{\bk_4,\uparrow}}^{\equiv H_\text{int}} $$

• Take interaction between the two species to be attractive $U_0<0$

• Ground state of non-interacting problem is

$$ \ket{\text{FS}}=\prod_{|\bp|<k_\text{F}} \adop_{\bp\uparrow}\adop_{-\bp\downarrow}\ket{\text{VAC}}. $$

Application of interaction Hamiltonian $H_\text{int}$ generates terms of form $$ \adop_{\bp+\bq\uparrow}\adop_{-\bp\downarrow}\aop_{-\bp'\downarrow}\aop_{\bp'+\bq\uparrow}\ket{\text{FS}} $$ with $|\bp|,|\bp+\bq|>k_\text{F},|\bp'|,|\bp'+\bq|<k_\text{F}$

• Note difference from Bose case: don’t just create pair excitations with zero centre of mass momentum $\bq=0$

• Nevertheless, BCS theory makes assumption that ground state involves a superposition of zero momentum pairs only

• We can write such a state very generally as

$$ \ket{\text{pair}}\equiv\sum_{\sum_\bp n^P_\bp=N/2} c_{{n^P_{\bp}}} \prod_{\bp}\left[\adop_{\bp\uparrow}\adop_{-\bp\downarrow}\right]^ {n_{\bp}}\ket{\text{VAC}} $$

• Restricting ourselves to states of this form means that $$ \braket{\text{pair}|H_\text{int}|\text{pair}} = \frac{U_0}{V}N_\uparrow N_\downarrow+\braket{\text{pair}|\tilde H_{\text{int}}|\text{pair}}, $$ where the first term is the Hartree–Fock energy and

$$ \tilde H_{\text{int}}=\frac{U_0}{V}\sum_{\bp, \bp’}\adop_ {\bp\uparrow}\adop_{-\bp\downarrow}\aop_{-\bp’\downarrow}\aop_{\bp’\uparrow}. $$

Why? There is some double counting of terms that is irrelevant as $V\to\infty$

• Introduce the pair operators $\bdop_\bp=\adop_{\bp\uparrow}\adop_{-\bp}$, $\bop_\bp=\aop_{-\bp,\downarrow}\aop_{\bp\uparrow}$

• For $\braket{\text{pair}|\cdots|\text{pair}}$ we can replace $H\to H_\text{pair}$ $$ H_{\text{pair}}=2\sum_{\bp}\epsilon_{\bp}\bdop_\bp\bop_\bp+\frac{U_0}{V}\sum'_{\bp,\bp'} \bdop_\bp \bop_{\bp'} $$ since $2\bdop_\bp\bop_\bp = \adop_{\bp,\uparrow}\aop_{\bp,\uparrow}+\adop_{-\bp,\downarrow}\aop_{-\bp,\downarrow}$ on these states

• Looks quadratic. Can we solve it?

• Nope! $\bdop_\bp$, $\bop_\bp$ don’t obey canonical Bose commutation relations

• Pair operators $\bop_\bp$ commute at different momenta $$ [\bop_\bp,\bop_{\bp'}]=[\bdop_\bp,\bdop_{\bp'}]=[\bdop_\bp,\bop_{\bp'}]=0\qquad \bp\neq\bp', $$ but obey the hardcore constraint $$ (\bdop_\bp)^2=0 $$ (can’t create two fermions in same state)

• Try variational state (pair amplitudes factorize c.f. Bogoliubov)

$$ \ket{N \text{ pair}}\equiv\left[\sum_\bp c_\bp \bdop_\bp\right]^{N/2}\ket{\text{VAC}} $$

• Energy expectation still tricky. For instance, what is the expectation value of the kinetic energy?

$$ \mathrm{K.E}=2\sum_\bp\epsilon_{\bp}\langle\bdop_\bp\bop_\bp\rangle\equiv 2\sum_\bp\epsilon_{\bp} \langle n^P_ \bp\rangle, $$

• Finding average number of pairs $\langle n^P_\bp\rangle$ not obvious

• BCS considered normalized wavefunction

$$ \ket{\text{BCS}} =\prod_\bp \left[v_\bp\bdop_\bp+u_\bp\right]\ket{\text{VAC}}\qquad |u_\bp|^2+|v_\bp| ^2=1. $$

• Superposition of states with different total number of particles

Projection to fixed number $N$ of particles matches $$ \ket{N \text{ pair}}\equiv\left[\sum_\bp c_\bp \bdop_\bp\right]^{N/2}\ket{\text{VAC}} $$ if $c_\bp=v_\bp/u_\bp$.

• $\langle n^P_\bp\rangle= v_\bp^2$ and total variational energy of this state is

$$ \braket{\text{BCS}|H|\text{BCS}}=2\sum_\bp \epsilon_{\bp}|v_\bp|^2+\frac{U_0}{V}\sum_{\bp,\bp'}u^*_\bp v_ \bp u_{\bp'}v^*_{\bp'}. $$

Show this

How about that non-conserving wavefunction?

• Expectation of any particle number conserving operator is $$ \braket{\text{BCS}|\co|\text{BCS}}=\sum_N P_N \braket{N \text{ pair}|\co|N\text{ pair}}, $$

• The probabilities $P_N$ are $$ P_N=\sum_{\sum n^P_\bp=N/2}\prod_\bp \left[n^P_\bp |v_\bp|^2+\left(1-n^P_\bp\right)|u_\bp|^2 \right], $$

$$ P_N=\sum_{\sum n^P_\bp=N/2}\prod_\bp \left[n^P_\bp |v_\bp|^2+\left(1-n^P_\bp\right)|u_\bp|^2 \right] $$

• Distribution strongly peaked around $$ \langle N \rangle=2\sum_\bp |v_\bp|^2=2\sum_\bp \langle n^P_\bp \rangle $$ with a variance that is $O(N)$. Thus at large $N$

$$ \braket{\text{BCS}|\co|\text{BCS}}\to \braket{\langle N\rangle \text{ pair}|\co|\langle N\rangle\text{ pair}} $$

Anderson spin chain

• $\bop_\bp$, $\bdop_\bp$, and $\bdop_\bp\bop_\bp-1/2$ behave as the components of a spin-1/2 $$ S_\bp^+ \equiv \bdop_\bp,\quad S_\bp^- \equiv \bop_\bp,\quad S^z_\bp = \bdop_\bp\bop_\bp-1/2, $$ on account of the commutation relations (Anderson spins)

$$ \left[\bdop_\bp,\bop_\bp\right]=2\left(\bdop_\bp\bop_\bp-1/2\right)\nonumber\ \left[\bdop_\bp,\left(\bdop_\bp\bop_\bp-1/2\right)\right]=-\bdop_\bp. $$

• $H_\text{pair}$ is a spin chain $$ H_{\text{pair}}-\mu N=2\sum_\bp \xi({\bp})S_\bp^z+\frac{U_0}{V}\sum_{\bp,\bp'}S^+_\bp S^-_{\bp'}, $$ where we included chemical potential by defining $\xi_\bp\equiv\epsilon(\bp)-\mu$.

• Parameterize $$ \left(u_\bp,v_\bp\right)=(\cos(\theta_\bp/2)e^{-i\varphi_\bp/2},\sin(\theta_\bp/2)e^{i\varphi_\bp/2}) $$ then the variational energy is (except for a constant) $$ \braket{\text{BCS}|H|\text{BCS}}=-\sum_\bp \xi_\bp\cos\theta_\bp+\frac{U_0}{4V}\sum_{\bp,\bp'}\sin \theta_\bp\sin\theta_{\bp'}\cos\left(\varphi_\bp-\varphi_{\bp'}\right) $$

• Interpretation

  1. First term tends to align spins with z-axis in - direction for $\xi_\bp<0$ and in + direction for $\xi_\bp>0$

  2. Second term – from attractive $H_\text{int}$ – wants the spins to lie in the x-y plane

Minimize energy

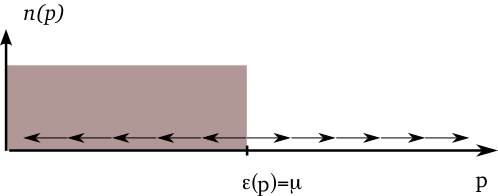
• For $U_0>0$ (repulsive interactions), spins all point in $\pm z$ direction, forming ‘domain wall’ where $\xi_{\bp}$ changes sign at Fermi surface

• Relationship between spin picture and average number of pairs is $$ \langle n^P_{\bp}\rangle=v_\bp^2=\left[1-\cos\theta_\bp\right]/2, $$ so this corresponds to sharp Fermi step.

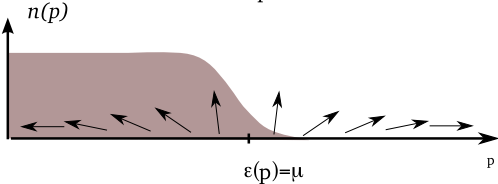
• For $U_0<0$, system can lower its energy by taking $\sin\theta_\bp\neq 0$

• Lowering of interaction energy more than compensates increase in kinetic energy that comes from smearing the step

• All angles $\varphi_\bp$, describing angle in x-y plane, should be equal

$$ \braket{\text{BCS}|H|\text{BCS}}=-\sum_\bp \xi_\bp\cos\theta_\bp+\frac{U_0}{4V}\sum_{\bp,\bp'}\sin \theta_\bp\sin\theta_{\bp'} $$

• Taking the extremum of energy with respect to angles $\theta_{\bp}$ gives $$ \xi_{\bp}\sin\theta_\bp-|\Delta|\cos\theta_\bp=0, $$ where the gap parameter is $$ \Delta=-\frac{U_0}{2V}\sum_\bp e^{i\varphi}\sin\theta_\bp=-\frac{U_0}{V}\sum_\bp u_\bp v^*_\bp. $$ $$ \cos\theta_\bp=\frac{\xi_{\bp}}{E_\bp},\qquad \sin\theta_\bp=\frac{|\Delta|}{E_\bp}, \qquad E_\bp=\sqrt{\xi (\bp)^2+|\Delta|^2} $$

• Solution corresponds to alignment of spin vector with the direction of the effective `magnetic field’

$$ \left(\mathrm{Re},\Delta.\mathrm{Im},\Delta,\xi_\bp\right) $$

• To be self-consistent, must satisfy the gap equation $$ \Delta=-\frac{U_0}{2V}\sum_\bp \frac{\Delta}{E_\bp} $$ with continuum limit $$ \Delta=-\frac{U_0}{2}\int \frac{d\bp}{\left(2\pi\right)^3} \frac{\Delta}{E_\bp} $$

$$ \Delta=-\frac{U_0}{2}\int \frac{d\bp}{\left(2\pi\right)^3} \frac{\Delta}{E_\bp} $$

• For $U_0>0$ there are no non-trivial solutions ($\Delta=0$ always)

• For any $U_0<0$ there is always a solution at finite $\Delta$.

• Integral divergent at high $\bp$. More significantly, for small $\Delta$, RHS is $$ \sim-\frac{U_0}{2}\nu(\mu)\Delta\log \Lambda/\Delta, $$ $\Lambda$ is high energy cut-off and $\nu(\mu)$ is density of states per spin

• No matter how small the attraction $U_0<0$, always a solution with finite $\Delta$. This is the Cooper phenomenon.

Quasiparticle Excitations

• Like Bogoliubov, BCS theory also lets us discuss excitations

• Can solve BCS hamiltonian by Bogoliubov (we didn’t) but can introduce Bogoliubov-type excitations after the fact

$$ \ket{\text{BCS}} =\prod_\bp \left[v_\bp\adop_{\bp\uparrow}\adop_{-\bp\downarrow}+u_\bp\right]\ket{\text{VAC}} $$

• Can show that $$ \begin{align*} \alop_{\bp\uparrow}&=u_{\bp}\aop_{\bp\uparrow}-v_{\bp}\adop_{-\bp\downarrow}\\ \alop_{\bp\downarrow}&=u_{-\bp}\aop_{\bp\downarrow}+v_{-\bp}\adop_{-\bp\uparrow}, \end{align*} $$ satisfy fermion anticommutation relations and annihilate BCS state $$ \alop_{\bp,s}\ket{\text{BCS}}=0. $$

$$ \ket{\bp,s}=\aldop_{\bp,s}\ket{\text{BCS}}=\adop_{\bp,s}\prod_{\bp’\neq \bp} \left[v_{\bp’}\adop_ {\bp’\uparrow}\adop_{-\bp’\downarrow}+u_{\bp’}\right]\ket{\text{VAC}}, $$

• If we chose $s=\uparrow$ so that $\left(\bp,\uparrow\right)$ state is certainly occupied it means that $\adop_{\bp \uparrow}\adop_{-\bp\downarrow}\ket{\bp,\uparrow}=0$

• Corresponding term no longer appears in interaction term when it is applied to this state

• The level is said to be `blocked’. Thus it certainly is an eigenstate of the pair problem, if $\ket{\text{BCS}}$ is. What is its energy?

• Have to take into account kinetic energy as well as loss of attractive interaction energy

$$ E_{s}(\bp)=\xi_{\bp}[\overbrace{\left(1-\langle n^P_\bp\rangle\right)}^{\left(\bp,s\right),\mathrm{occupied}} \overbrace{-\langle n^P_\bp\rangle}^{\left(-\bp,-s\right),\mathrm{empty}}]+\overbrace{\Delta\sin\theta_ \bp}^{\mathrm{`blocking’}}=E_{\bp} $$

• These quasiparticle excitations always have a gap $\Delta_{s}$ given by

$$ \Delta_s=\min_\bp E_\bp=\begin{cases} \Delta, & \mu>0,\ \sqrt{\Delta^2+\mu^2},& \mu<0. \end{cases} $$

Features of the quasiparticle dispersion